
关于LCA的几个想法
昨天在zxz的提示下我去补了LCA(最近公共祖先),有感而作
1.学习
在我学习LCA的时候,遇到不会的,我直接选择的了逃避……直接学
习其他博主写的code。导致我到最好也没有学到什么东西……
所幸,我始终有很好的同学的来指出的我的错误
(在这里悄悄感谢他们) 于是有了2
2.思考
正文开始:
我们在LCA函数中是要让两个孩子不不断上升的,最后找到他们的
(爹) 祖先, 于是乎,怎么来迫近这个祖先呢:
我有如下想法 ### 1.朴素
首先我们是在一个多叉树上找找祖先的,那么有个性质节点的父节点的
==深度(depth)== 为该节点 ==-1== (应该)
那么我们可以把不在同一层的孩子上升的到节点(根据深度差),然后依次同步向上,直到重合,
==第一个重合的点== 自然就是最近公共祖先啦 (以上做法毕竟朴素,容易TLE
(寄掉) ) ### 2倍增
(又到了人见人爱(詪)的倍增了……
用倍增,一半就不会TLE了,在预处理(把孩子上升到同一高度上)和不断上升进行了优化,
talk is cheap,show me your code 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37 int LCA(int al, int bl) {
//there: make depth[al] < depth[bl]
//=== al higher than bl
if (depth[al] > depth[bl]) {
swap(al, bl);
}
int x_h = depth[bl] - depth[al];
for (int i = 0; i <= 20; i++) {
if (x_h & (1 << i)) {
//用(1<<i)的原因是f[][i]这个第二的数组条件是二进制表示的
bl = father[bl][i];
}
}
if (al == bl) {return al;}
for (int i = 19; i >= 0; i--) {
if (father[al][i] != father[bl][i]) {
//只要是公共祖先那么就向下
//直到不是公共祖先,那么该点的父亲就是最近公共祖先
//逆向思维,妙啊§(* ̄▽ ̄*)§
al = father[al][i];
bl = father[bl][i];
}
}
return father[bl][0];
//朴素:
// for (int i = 1; i <= x_h; i++) {
// bl = father[bl][0];
// }
// for (int i = 1; i < 20; i++) {
// if (al == bl) {return al;}
// al = father[al][0];
// bl = father[bl][0];
// }
}
前方核聚变打击警告!!!__
:下面就昨天晚上睡不着觉想的…… ### 3. 不怕犯错 *** 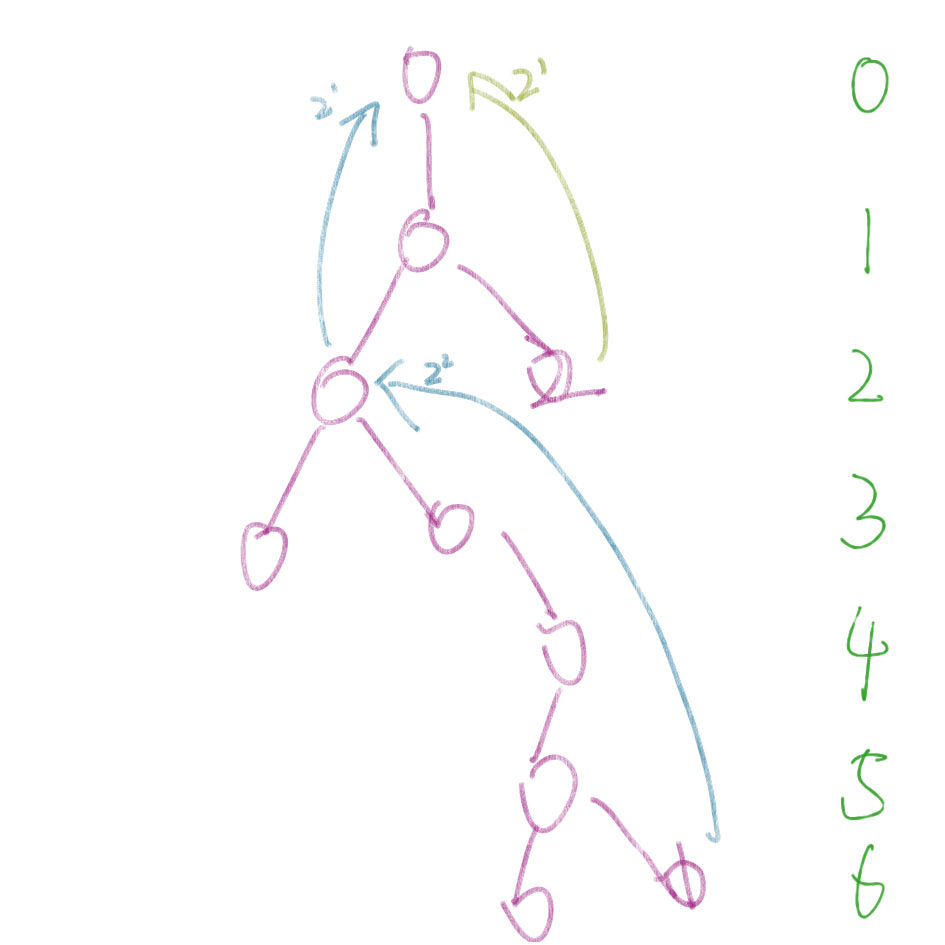
新建vis[]判断是否访问过,两个last_place 记录上一次节点。 step 1.
先用倍增不断向上,直到访问过或者到顶,(按理说,到了根节点也是最坏情况,也算一种访问过)
*** 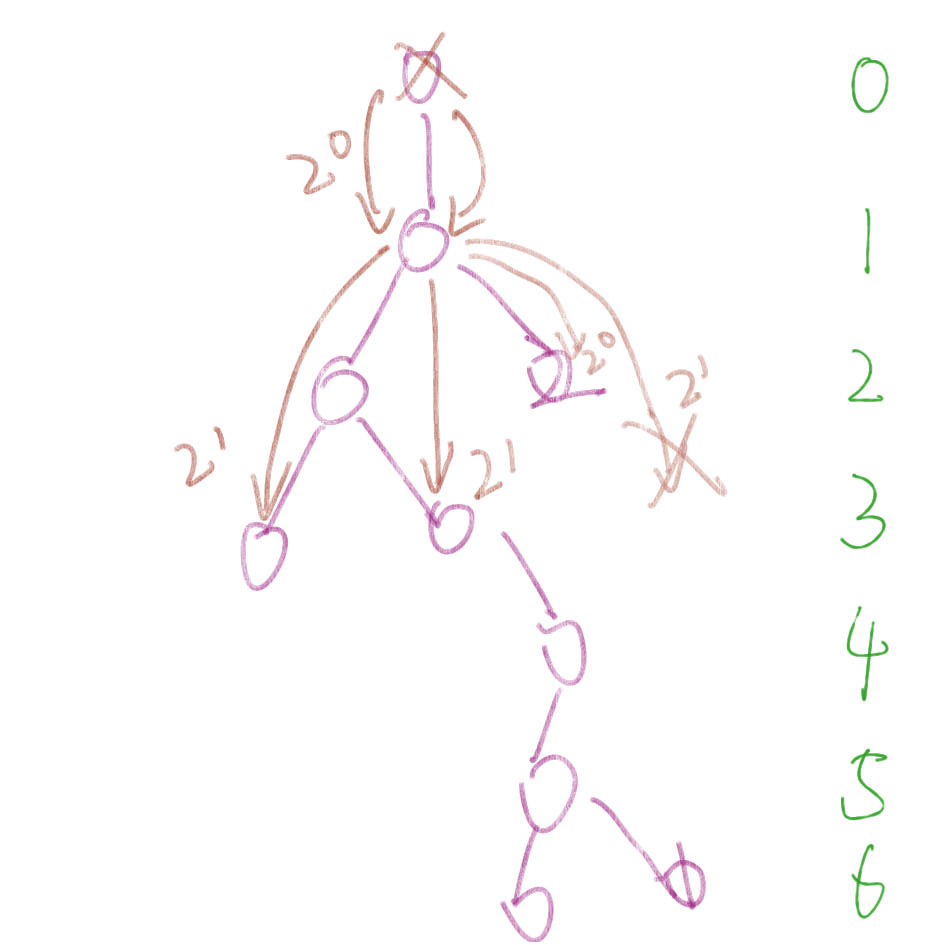
step 2. 然后向下倍增(从小开始),知道两个点分别向下的后的节点不同,再返回上一个相同点。 从上一个相同点重新开始向下倍增,知道2^0的点不相同,那么当前节点就是最近公共祖先; step 3. 然后就是在边界上处理一下,(感觉也没有快多少,反而更难实现了……QwQ
没关系,不怕犯错! ### 小聪明
把两个孩子到根节点的路径遍历一边,将记录到一个数组中国,
然后sort一下(应该需要把……) 然后进行伪去重(应该是unique();
然后直接找最后一个就行嘿嘿……
补:好像 unique(); ,不是很行……,手写吧……