〔20221020〕考试改题笔记

发表于 更新于
发现还是有很多基础的东西我不会,在此记录

T1 部落(tribe)

  说实话我知道用最长上升子序列,但是我已经好长时间没有打过了,为了保底,我直接来了暴搜(从顶向左右山脚更新) 然后……寄了

  最后还是乖乖复习了最长上升子序列 和看题解 这里感谢 @psq对我的支持

最长上升子序列:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int zzsszxl(int l,int r){
    memset(f,0,sizeof(f));
    f[l]=in[l];
    int len=1;
    for(int i=l+1;i<=r;i++){
        if (in[i]>=f[len]){f[++len]=in[i];}
        else{
            int pos=upper_bound(f+1,f+len+1,in[i])-f;
            f[pos]=in[i];
        }
    }
    return len;
}
//如果是求最长(单调)下降子序列的话,我们可以直接取相反数,减少码量

T2传递（transfer）

  考试的时候我写的模拟,但是……炸了QwQ

其实大模拟也能过

有如下accepted代码

code 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
using namespace std;
int n, h;
int f[1010];
int in[1010];
int read();
int zzsszxl(int l, int r) {
    memset(f, 0, sizeof(f));
    f[l] = in[l];
    int len = 1;
    for (int i = l + 1; i <= r; i++) {
        if (in[i] >= f[len]) {f[++len] = in[i];}
        else {
            int pow = upper_bound(f + 1, f + len + 1, in[i]) - f;
            f[pow] = in[i];
        }
    }
    return len;
}
int main() {
    // freopen("in.txt","r",stdin);
    freopen("tribe.in", "r", stdin);
    freopen("tribe.out", "w", stdout);
    n = read(), h = read();
    for (int i = 1; i <= n; i++) {
        in[i] = read();
    }
    int temp = zzsszxl(1, h);
    for (int i = h; i <= n; i++) {
        in[i] = (-in[i]);
    }
    int temp2 = zzsszxl(h, n);
    printf("%d\n", n - temp - temp2);
    return 0;
}

int read() {
    int x = 0, w = 1; char ch = 0;
    while (ch < '0' || ch > '9') {  if (ch == '-') w = -1; ch = getchar();}
    while (ch >= '0' && ch <= '9') { x = x * 10 + (ch - '0'); ch = getchar();}
    return x * w;
}

  不得不说优化就是玄学,我之前开O3(G++和GCC),(后来@ymj指出没有只有GCC管用) 我第一交的时候开了G++的,交上去TLE了

我：把G++那一行删去了,然后就accepted

删之前
删之后

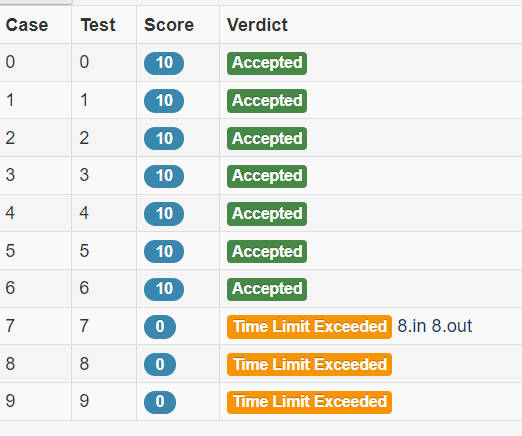
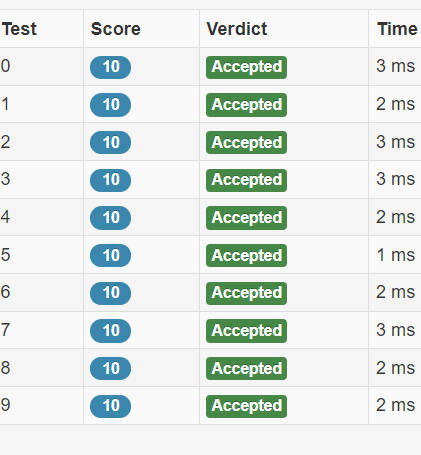
就很神奇啊,玄学……

T3 光 (light)

  这题本来还没看的时候,听到@ymj说是差分约束。(我还以为我赚到了) 没想到考完试问他,他说他说错了……。我:………………

  QwQ,我考场上想了好久,就是很难把他转化到图上……这提醒我们要自己做题,不要受他人感染。我就是最好的例子QwQ💔

最后我就打出来 \(O(N^{4})\) 的,我其实还写了DFS的,结果不知道说明情况炸了QwQ。最后考完的时候听@wfy才想起来可以优化到 \(O(N^3)\) 的(从前三个推出第四个……)

正解是在这个优化上,根据题目的某些玄学性质,二分第三个…… (别人的正解前面有几个玄学的swap,但是我不加就不过,玄学,确实玄学……)

明天应该还有一场,再接再厉吧……

🍂全文完↩︎